파티클 필터는 베이즈 필터에 몬테카를로 시뮬레이션 아이디어를 결합한 추정 알고리즘이다.

파티클 필터
파티클 필터는 적분을 수치적으로 근사하기 위해 확률 분포를 파티클 집합으로 표현한다. 즉, 확률 분포를 직접 계산하는 대신 샘플 기반으로 근사하는 방법이다.
각 파티클은 상태 공간에서 하나의 상태 후보를 나타내며, 새로운 관측값이 들어올 때마다 적합도를 평가하고 갱신한다. 이후, 재샘플링 과정을 통해 파티클 분포를 조정하여 보다 정확한 상태 추정을 수행한다.
예측(Prediction)
우리는 시스템 모델을 바탕으로, k 번째 상태를 예측할 수 있다. 만약 1000개의 파티클(상태 후보)가 있다면, 시스템 모델을 사용하여 1000개의 파티클의 다음 상태를 예측하는 것이다.
이전 스텝에서 i 번째 파티클: x(i)k-1
예측된 i 번째 파티클: x(i)k | k-1
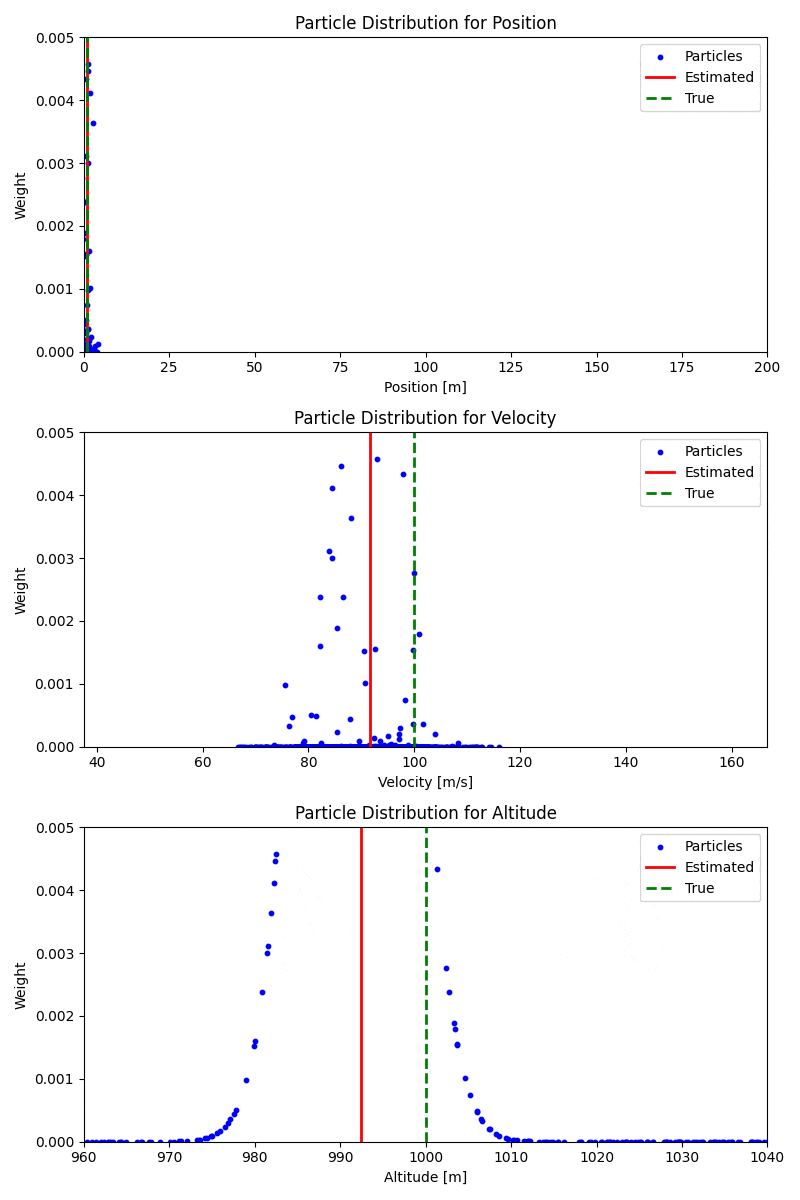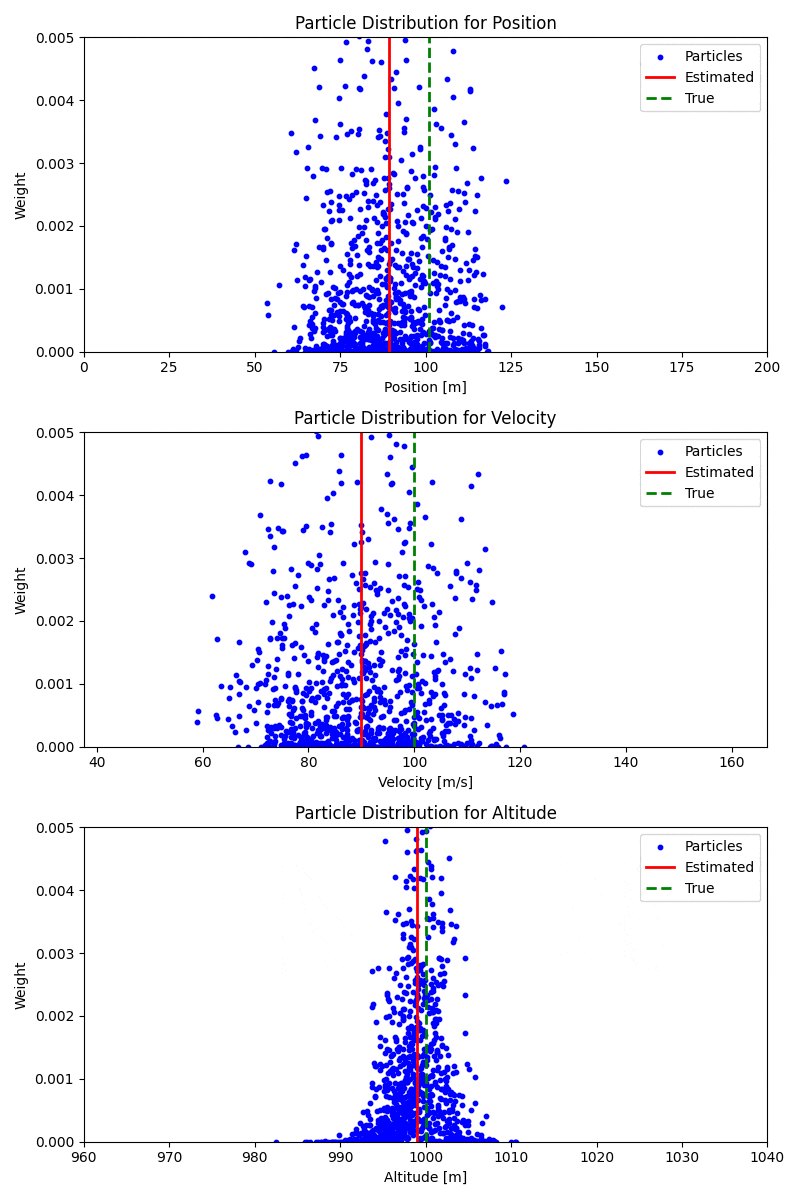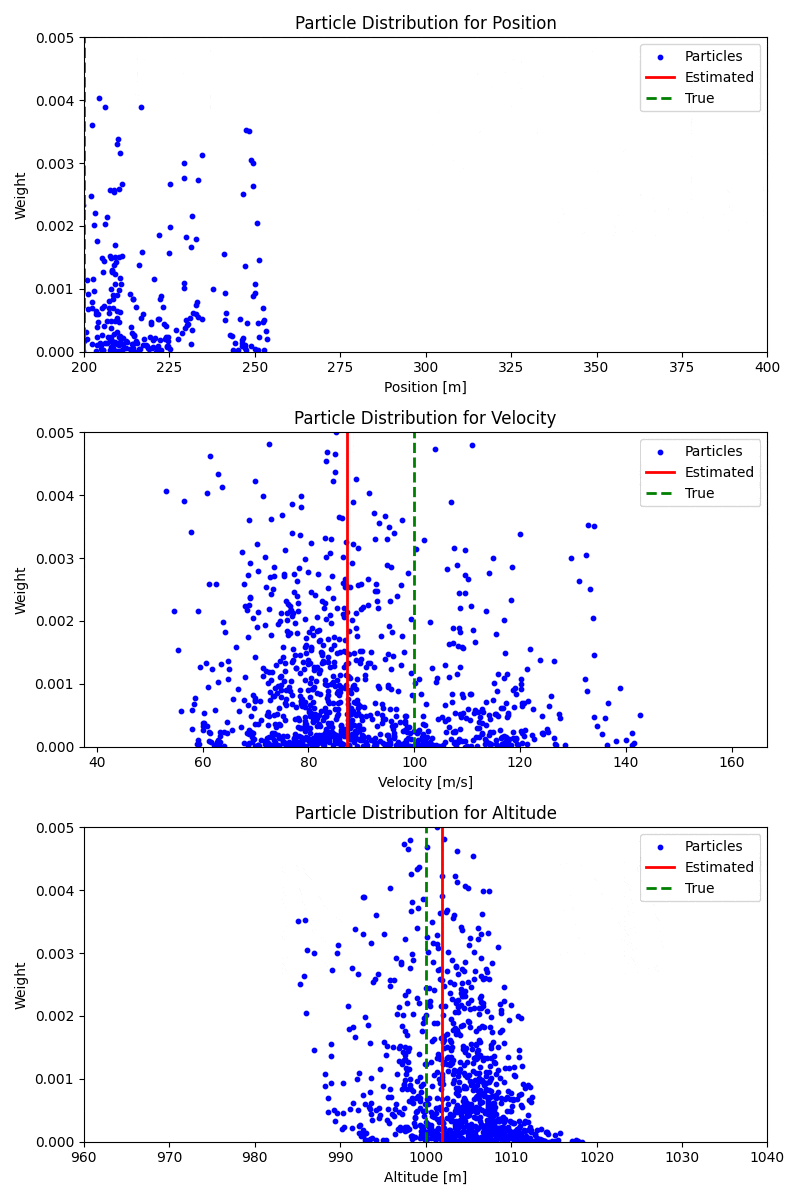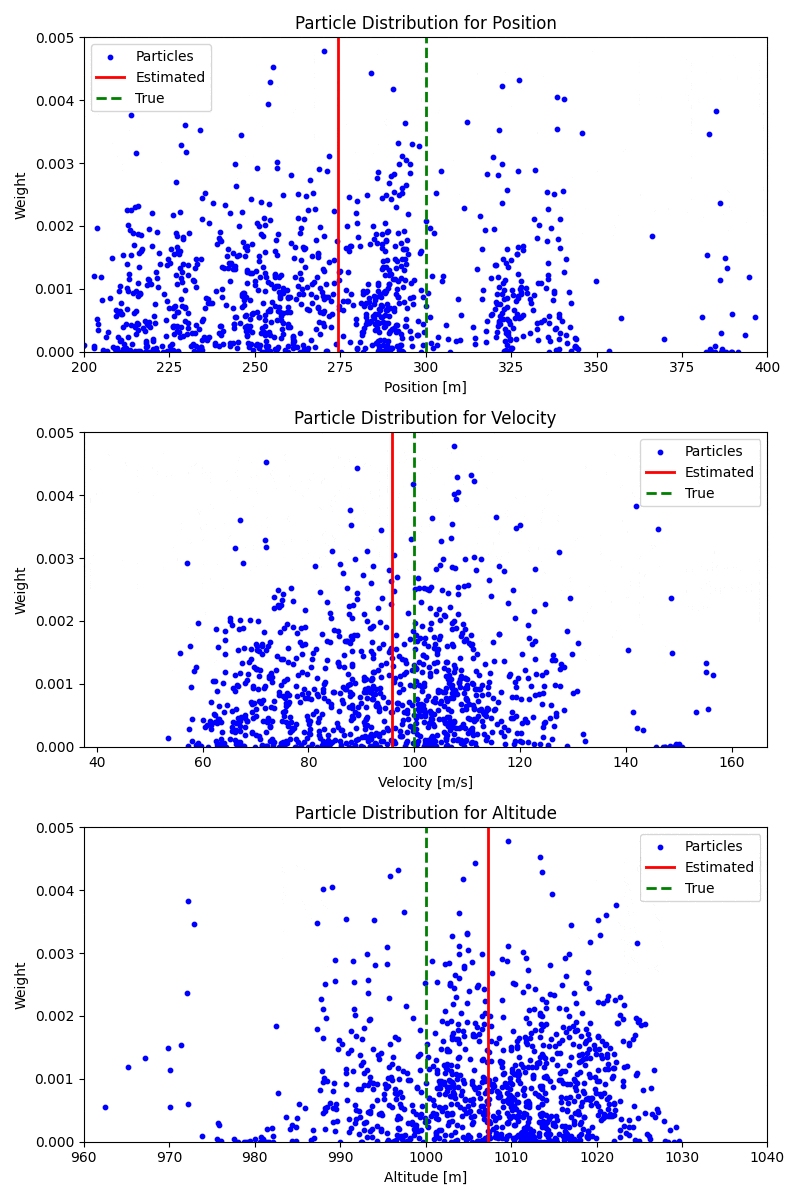
다음 사진에서 막대그래프의 x축은 각 파티클이 예측한 상태이고, 막대그래프의 높이는 파티클의 가중치(상태 후보의 적합도)이다. 예시 사진은 8번째 스텝에서 예측된 파티클로 근사 된 분포와 True State이다. 이때 가중치(막대그래프의 높이)는 아직 업데이트되기 전이다.

업데이트(Update)
파티클 필터의 업데이트 단계는 다음과 같다.
1. 관측치 zk 에 대한 우도(Likelihood) 계산
우도(Likelihood)는 관측치를 고정한 상태에서 분포를 변화시키며, 어떤 분포가 관측치를 가장 잘 설명하는지 평가하는 개념이다. 여기서 분포는 가우시안 분포로 가정하며, 평균은 각 파티클에 의해 예측된 관측치 Hxk | k-1, 분산은 사용자 지정 파라미터로 설정된다.
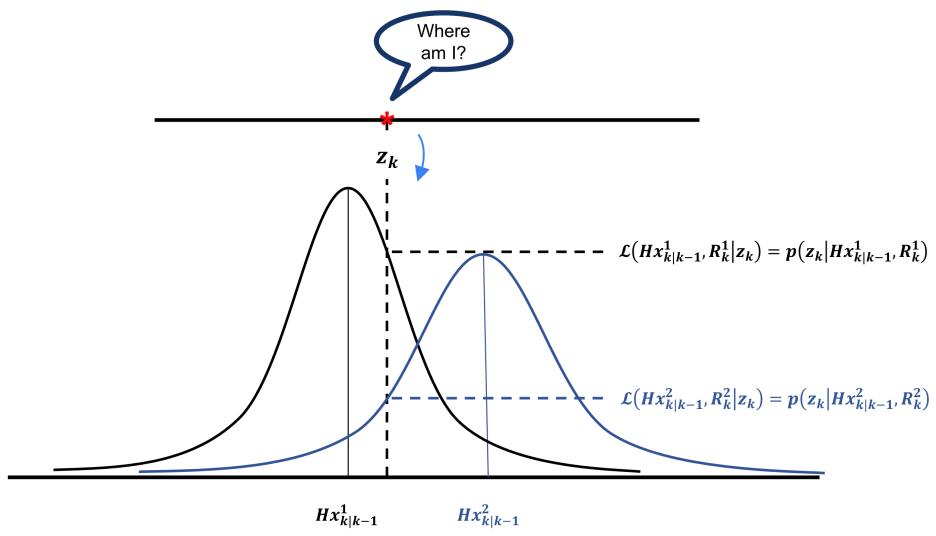
위 그림은 두 개의 파티클을 기반으로 생성된 가우시안 분포에서, 고정된 관측치에 따른 강도를 나타낸 것이다. 만약 분포의 평균이 관측치와 가까울수록, 해당 분포가 관측치를 보다 잘 설명한다고 볼 수 있다.
2. 이전 가중치에 우도를 곱하여 업데이트
가중치는 각 파티클의 적합도를 의미하는데, 우도를 사용하여 이를 업데이트한다. 특정 파티클로 생성한 가우시안 분포에서 관측치의 강도가 높다면 해당 파티클의 적합도는 높아지고, 관측치의 강도가 낮아지면 해당 파티클의 적합도는 낮아진다.
3. 업데이트된 가중치를 정규화
업데이트된 분포를 정규화하여, 전체 확률의 합이 1이 되도록 보장한다. 다음 그림은 관측치 입력 후 갱신된 파티클 분포를 나타낸다. 각 파티클의 가중치는 우도를 기반으로 조정되며, 이를 통해 이전에 예측된 분포가 관측치 방향으로 업데이트된 것을 확인할 수 있다.

4. 추정 상태 계산
가중치합은 1로 이미 정규화되었다. 따라서 사후확률 분포의 기댓값을 계산하면 최종 추정 상태를 얻을 수 있다.
전체 글은 아래 네이버 블로그에서 확인해주세요.https://m.blog.naver.com/rlarlarlathgus/223788850202
파티클 필터(Particle Filter)
파티클 필터는 베이즈 필터에 몬테카를로 시뮬레이션 아이디어를 결합한 추정 알고리즘이다. 베이즈 필터는...
blog.naver.com